Gauss Found the Way
“What is the sum of the first one hundred numbers beginning from one?”
(i.e. 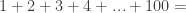 ?)
?)
After the teacher asked this question, the class, which was full of young kids, fell into complete silence. A few students were stunned by the seemingly-impossible challenge and readily gave up; most students began scribbling on the paper, trying to add all the numbers one by one, from the very beginning. What a difficult question! They thought.
But there was one kid in the class did it differently. He thought about it for a few minutes, did some simple calculation, and raised his hand.
“I am finished,” the student said.
“How is it possible,” the teacher said to himself as he walked toward the student, “the problem would take one at least an hour to do!” Indeed, if he had solve the problem himself, he would just sum up all the one hundred numbers one by one as well – as a matter of fact, he presented the problem to the class just to kill some time. But after he examined his student’s answer, he was shocked.
“It’s a genius’ solution!” after a few seconds of freezing in astonishment, the teacher shouted, “this kid is going to be famous!”
It was in the late 18th century, Germany. The teacher was right – it turned out to be that his brilliant student, Johann Carl Friedrich Gauss, became one of the most famous and important mathematicians of all time.
So, how did young Gauss do the calculation?
First, he wrote the sum twice, one in an ordinary order and the other in a reverse order:
1 + 2 + 3 + 4 + . . . + 99 + 100
100 + 99 + . . . + 4 + 3 + 2 + 1
100 + 99 + . . . + 4 + 3 + 2 + 1
By adding vertically, each pair of numbers adds up to 101:
| 1 | + | 2 | + | 3 | + | . . . | + | 98 | + | 99 | + | 100 |
| 100 | + | 99 | + | 98 | + | . . . | + | 3 | + | 2 | + | 1 |
| 101 | + | 101 | + | 101 | + | . . . | + | 101 | + | 101 | + | 101 |
Since there are 100 of these sums of 101, the total is 100 X 101 = 10,100. Because this sum 10,100 is twice the sum of the numbers 1 through 100, we have: